Ecuaciones Diferenciales: 4. Sistemas de Ecuaciones Diferenciales Lineales

Un sistema de ecuaciones diferenciales es un conjunto de varias ecuaciones diferenciales con varias funciones incógnitas y un conjunto de condiciones de contorno. Una solución del mismo es un conjunto de funciones diferenciables que satisfacen todas y cada una de las ecuaciones del sistema. Según el tipo de ecuaciones diferenciales pude tenerse un sistema de ecuaciones diferenciales ordinarias o un sistema de ecuaciones en derivadas parciales.
En un sistema de ecuaciones diferenciales ordinarias de cualquier orden, puede ser reducido a un sistema equivalente de primer orden, si se introducen nuevas variables y ecuaciones. Por esa razón en este artículo sólo se consideran sistemas de ecuaciones de primer orden. Un sistema de ecuaciones diferenciales ordinarias de primer orden escrito en forma explícita es un sistema de ecuaciones de la forma:
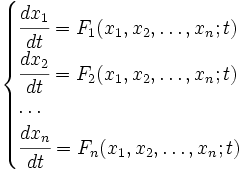
$\begin{cases} \cfrac{dx_1}{dt} = F_1(x_1,x_2,\ldots,x_n;t)\\ \cfrac{dx_2}{dt} = F_2(x_1,x_2,\ldots,x_n;t)\\ \ldots \\ \cfrac{dx_n}{dt} = F_n(x_1,x_2,\ldots,x_n;t) \end{cases}$
Reducción a un sistema de primer orden
Dado un sistema de ecuaciones diferenciales de orden n con m ecuaciones:

$F_i\left(x_j,\frac{dx_j}{dt},\ldots,\frac{d^nx_i}{dt^n};t\right) =0 \qquad \mbox{con}\ i,j\in\{1,2,\ldots,m\}$

Existe un sistema equivalente de primer orden con a lo sumo (n+1)xm ecuaciones. Para ver esto consideremos un sistema en que intervienen m funciones incógnitas x_i y sus n derivadas, e introduzcamos un nuevo conjunto de variables y_i,k definidos de la siguiente manera:

$y_{i,k}(t) := \frac{d^k x_i(t)}{dt^k}$

El sistema de primer orden equivalente en las variables y_i,k resulta ser:

$\begin{cases} y_{i,k+1} = \cfrac{dy_{i,k}}{dt} & k\in\{0,2,\ldots,n-1\}\\ F_i\left(y_{j,0},y_{j,1},\ldots,y_{j,n};t\right) =0 & i,j\in\{1,2,\ldots,m\} \end{cases}$

Como ejemplo de reducción de un sistema de ecuaciones diferenciales podemos considerar las ecuaciones de movimiento de la mecánica newtoniana de una partícula que es un sistema de segundo orden con tres ecuaciones:

$\begin{cases} m\cfrac{d^2x}{dt^2} = F_x\left(x,y,z;\cfrac{dx}{dt},\cfrac{dy}{dt},\cfrac{dz}{dt};t\right)\\ m\cfrac{d^2y}{dt^2} = F_y\left(x,y,z;\cfrac{dx}{dt},\cfrac{dy}{dt},\cfrac{dz}{dt};t\right)\\ m\cfrac{d^2z}{dt^2} = F_z\left(x,y,z;\cfrac{dx}{dt},\cfrac{dy}{dt},\cfrac{dz}{dt};t\right) \end{cases}$

Si se introducen tres funciones incógnita nuevas que representan la velocidad, el sistema anterior se puede reducir a un sistema de primer orden y seis ecuaciones:

$\begin{cases} m\cfrac{dx}{dt} = v_x(t), & m\cfrac{dv_x}{dt} = F_x\left(x,y,z;v_x,v_y,v_z;t\right)\\ m\cfrac{dy}{dt} = v_y(t), & m\cfrac{dv_y}{dt} = F_y\left(x,y,z;v_x,v_y,v_z;t\right)\\ m\cfrac{dz}{dt} = v_z(t), & m\cfrac{dv_z}{dt} = F_z\left(x,y,z;v_x,v_y,v_z;t\right) \end{cases}$

Ecuaciones Diferenciales

miércoles, 27 de junio de 2012

4. Sistemas de Ecuaciones Diferenciales Lineales

No hay comentarios:

Publicar un comentario